Bifurkationsdiagram är väldigt intressanta, och vad som i synnerhet fångade mitt intresse är logistisk bifurkation. Det bygger på en enkel ekvation skapad av Pierre François Verhulst för att undersöka populationer av djur, hur mycket de reproducerar och om och när de svälter.
"where xn is a number between zero and one that represents the ratio of existing population to the maximum possible population. The values of interest for the parameter r (sometimes also denoted μ) are those in the interval [0,4]."
Men något helt bisarrt händer över tid, om r är lägre än 4:
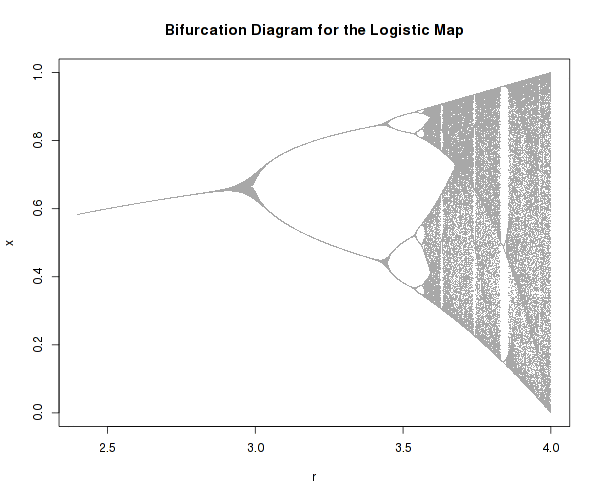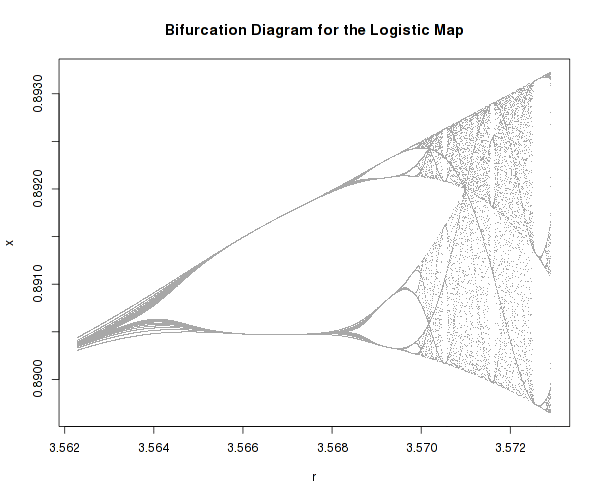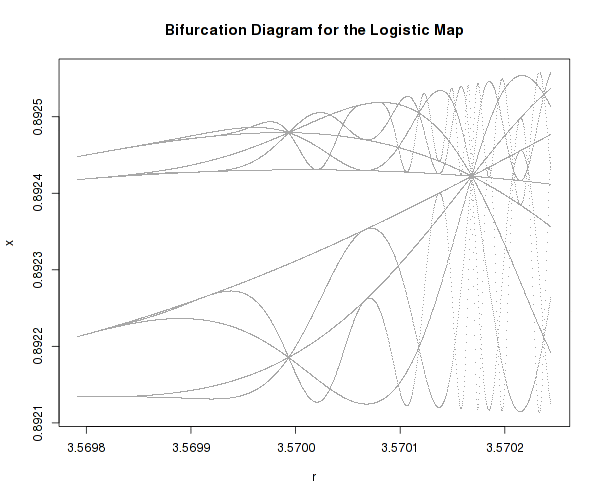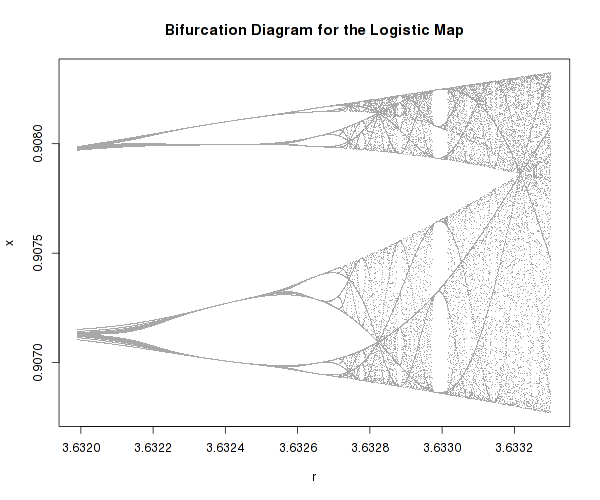
De tydliga förutsägbara populationerna blir helt och hållet kaotiska och på diagramet bildar vackra, nästan organiska landskap av unika tal.
Jag visste när jag lärde mig om det här att jag bara måste basera nummergeneratorn för pseudo-slumpmässiga tal i mitt spel på just bifurkation.
Det kallas pseudo-slumpmässiga tal eftersom datorer är inte bra på riktig slump. Inte för att det finns någon välbevisad teori för vad slump överhuvud taget är, det är något vi brukar kalla produkten av kaotiska system vi inte kan förutspå resultaten av med någon vidare säkerhet. Men inom programmering kallar man den slumpen en dator kan åstadkomma för pseudo-slump.
För mitt spel ville jag kunna få fram stora (decimal)tal som alltid ger samma nästledande tal. Men alltid unika talföljder om det första talet är unikt. Så alltså: samma ursprungstal, samma talföljd, annat ursprungstal, annan talföljd. Det är så möjligheten finns att röra sig frammåt och bakåt i talföljden för att skapa en slags karta av tal som kan navigeras beroende på situationen. Med andra ord, det är inte tärningskast som bara existerar i stunden och försvinner igen, eller tal som måste sparas på hårdisken varje gång det ska finnas kvar; utan tal som redan existerar i ekvationen och kan hittas igen om man har samma ursprungstal. Det är för många anledningar. Ett exempel är att kunna dela sitt ursprungstal, sitt seed som det kallas, så att andra spelare kan få samma värld genererad.
Här är en funktion, Lot(s), där man definerar s som ett tal mellan 0 till 1 och får resultatet av en bifurkation. Sen kan resultatet ploppas in i funktionen igen om man vill, och få nästa tal i talföljden.
När man bestämt s, så går s igenom Verhulst's ekvation vilket syns i rad två. Big betyder bara att talet inte är begränsat till de 15 decimaler programmeringsspråk vanligtvis är. Om jag lät det vara begränsat, skulle jag "bara" kunna få ut 1 000 000 000 000 000 olika tal.
s.e = -1 är för att berätta för Big att det stora talet är ett decimaltal. -1 placerar det stora talet "efter" ett heltal, dvs. som decimaler.
Problemet var nu att det logistiska bifurkationsdiagrammet inte är en balanserad tärning. Med det menar jag att den tenderar att ge ett ojämt antal nior, femmor osv., och jag ville att min tärning gav lika chans för alla nummer, som en bra tärning ska. Det är också för att jag ville att det ska kunna gå att använda dessa stora decimaltal som en andel i procent, för att avgöra slumpade sannolikheter i spelet. Då kan den inte vara obalanserad och ge över 90% en tredjedel av kasten.
Först funderade jag på ifall jag kunde lösa imbalansen med någon slags ekvation som motvikt. Men jag fick en idé som jag tyckte var enklare, och mycket elegantare. På rad fyra klipps den sista decimalen på det nya bifurkerade talet ut och klistras in i början av decimalerna. Som exempel med små decimaltal: 0.5534 förvandlas till 0.4553, 0.122 till 0.212, 0.0031 till 0.1003. Eftersom den sista decimalen är så gott som perfekt balanserat tärningskast så kan jag bara flytta den till början av talet och vips så har jag löst imbalansen. Talföljden blir annorlunda, men det är helt irrelevant eftersom det enda som behövs är att det finns en talföljd över huvud taget.
De sista två raderna begränsar talet till 200 decimaler och ger resultatet som en sträng.